Research Group
Heisenbergprofessur Arithmetische Geometrie
Professor
Prof. Dr. Alexander Ivanov
Email: alexander.ivanov(at)ruhr-uni-bochum.de
Phone: (+49)(0)234 / 32-19878
Team Members
Team Assistant
Annika Schulte
Email: annika.schulte(at)ruhr-uni-bochum.de
Phone: (+49)(0)234 / 32-22291
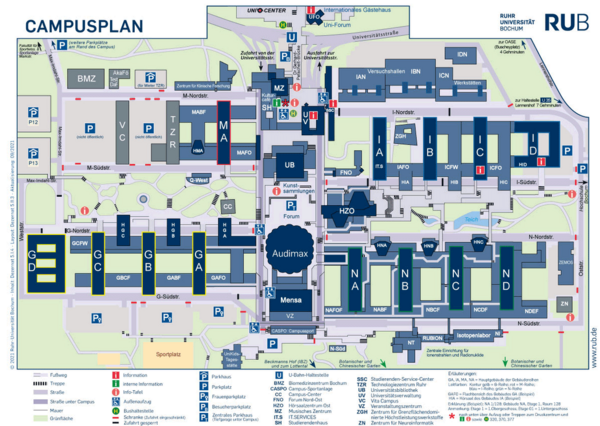
Address
Fakultät für Mathematik
Universitätsstr. 150
44801 Bochum
Building IB, Floor 2, Room 153 (Alexander Ivanov)
Building IB, Floor 2, Room 131 (Annika Schulte)